“La didáctica es específica de la disciplina. Cada disciplina tiene una epistemología y una naturaleza diferente. Los matemáticos puros interesados en la educación empezaron a hacer estudios epistemológicos del desarrollo de la matemática misma para decir que las matemáticas no se enseñan como se enseña literatura o biología.”
—— Reflexión sobre el trabajo pionero de Michèle Artigue
El Contexto Histórico
Michèle Artigue nació en 1946 en una pequeña aldea francesa, hija de una maestra de escuela elemental. Su brillante trayectoria académica la llevó desde el liceo rural, pedaleando diariamente seis kilómetros, hasta la prestigiosa École Normale Supérieure de Sèvres en París. Inicialmente formada como matemática pura en el campo de la lógica, Artigue se convirtió en una de las figuras más influyentes en la didáctica de las matemáticas.
Su transformación de matemática pura a investigadora en educación matemática ocurrió en 1970, cuando se unió al recién creado IREM de París bajo la dirección de André Revuz. Este instituto, surgido como consecuencia directa de los eventos de mayo de 1968 y las demandas de los “mathagrégibles”, representaba una nueva forma de abordar la educación matemática con rigor científico.
Artigue fue testigo y protagonista del nacimiento de la didáctica como disciplina científica autónoma, diferenciada tanto de la pedagogía general como de la matemática pura. Su trabajo pionero estableció las bases teóricas y metodológicas que transformarían la comprensión de cómo se enseñan y aprenden las ciencias.

La Revolución de los Años 60
El Nacimiento de la Didáctica
La didáctica de las matemáticas surgió en Francia durante los años 60, en pleno contexto de la carrera espacial hacia la luna. Los países buscaban acelerar su desarrollo científico y tecnológico, lo que llevó a la reforma de las matemáticas modernas a nivel mundial.
Esta reforma no fue solo un cambio curricular, sino el reconocimiento de que la educación matemática requería un enfoque científico específico, diferente de la pedagogía general y sustentado en:
- El análisis epistemológico de la disciplina
- La comprensión de los procesos cognitivos específicos
- El desarrollo de metodologías de investigación propias
- La colaboración entre matemáticos y educadores
En 1969 se crearon los primeros IREM (Institutos de Investigación sobre la Enseñanza de las Matemáticas) en Lyon, París y Estrasburgo. Estas instituciones, únicas en el mundo, establecieron el principio de colaboración entre matemáticos universitarios y profesores de secundaria, rompiendo jerarquías tradicionales en el espíritu de mayo del 68.
La Ingeniería Didáctica
Una metodología revolucionaria
Una de las contribuciones más significativas de Artigue fue el desarrollo de la ingeniería didáctica, metodología inspirada en el trabajo de los ingenieros que ella había observado durante su labor en la formación de ingenieros en matemáticas.
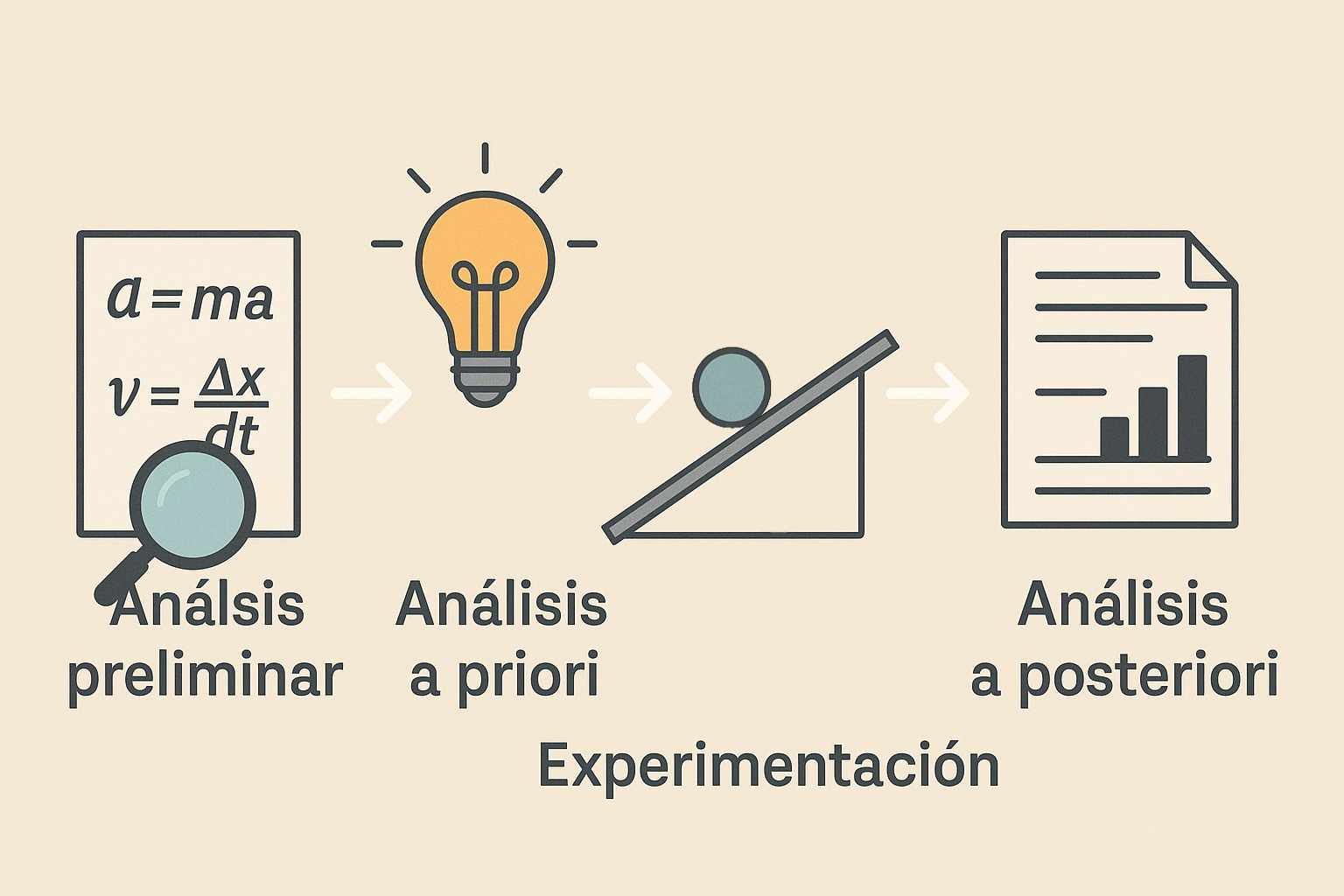
Esta metodología comprende cuatro fases fundamentales: el análisis a priori (que incluye la institución, el contenido y un análisis histórico-epistemológico), el diseño de actividades, la experimentación con estudiantes, y el análisis a posteriori que contrasta los resultados con las predicciones iniciales.
La ingeniería didáctica representó un salto cualitativo en la investigación educativa, proporcionando herramientas rigurosas para estudiar los fenómenos de enseñanza y aprendizaje en su complejidad natural, sin reducirlos a variables aisladas.
Epistemología vs Pedagogía
Artigue contribuyó decisivamente a establecer la distinción fundamental entre pedagogía y didáctica. Mientras la pedagogía agrupa a profesores de todas las disciplinas sin considerar las especificidades del contenido, la didáctica parte desde la disciplina misma, reconociendo que cada campo del conocimiento tiene su propia epistemología.
Los Pilares de la Didáctica Francesa
Sistémica: comprende la enseñanza como un sistema complejo donde estudiantes, profesores y conocimiento matemático interactúan.
Epistemológica: analiza la naturaleza y desarrollo histórico de los conceptos matemáticos para comprender los obstáculos de aprendizaje.
Contextual: considera que el aprendizaje es un proceso social que combina adaptación y aculturación.
Experimental: desarrolla investigación empírica manteniendo la complejidad del aula como centro del trabajo experimental.
El Desafío Interdisciplinario
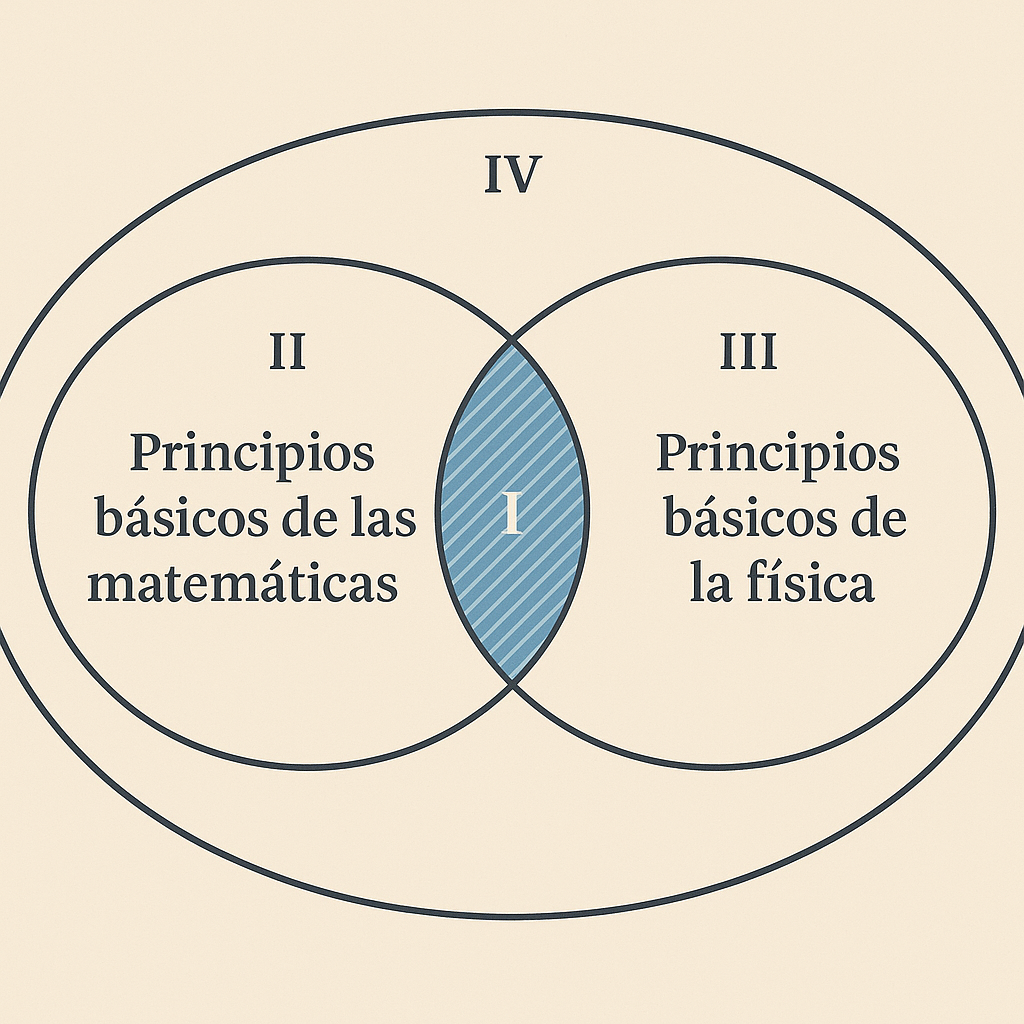
El trabajo de Artigue ilumina los desafíos actuales de la educación interdisciplinaria. Su colaboración con físicos como Laurence Viennot y Edith Saltiel en el proyecto experimental de matemáticas-física en la Universidad París 7 reveló tanto las posibilidades como las dificultades de integrar disciplinas.
La experiencia demostró que la interdisciplinariedad exitosa requiere que cada disciplina mantenga su rigor epistemológico. Como señaló Artigue, el único obstáculo insuperable que enfrentaron fue precisamente en el tema de diferenciales, donde matemáticos y físicos no lograron acordar una perspectiva común.
Esta tensión fundamental entre la especificidad disciplinaria y la integración interdisciplinaria permanece como uno de los grandes desafíos de la educación científica contemporánea.
Tecnología y Educación
Artigue fue pionera en el uso educativo de la tecnología, desarrollando el enfoque instrumental que reconoce la complejidad de transformar artefactos digitales en instrumentos matemáticos. Su trabajo con sistemas de álgebra computacional (CAS) en los años 90 demostró que la tecnología no elimina el trabajo técnico, sino que lo transforma, manteniendo la relación dialéctica esencial entre técnicas y conceptos.
Sus investigaciones revelaron que el discurso simplista sobre la tecnología educativa subestimaba los procesos de génesis instrumental necesarios para que estudiantes y profesores desarrollen competencias genuinas con herramientas digitales. Este enfoque influyó decisivamente en las políticas educativas francesas y internacionales sobre integración tecnológica.
Legado y Perspectivas
El impacto de Michèle Artigue trasciende las fronteras de Francia y las matemáticas. Como presidenta de la Comisión Internacional de Instrucción Matemática (ICMI) desde 2007 hasta 2010, promovió el reconocimiento internacional de la didáctica como campo científico maduro, estableciendo los premios Felix Klein y Hans Freudenthal para honrar la excelencia en investigación educativa.
Su visión sistémica, su rigor metodológico y su compromiso con la mejora de la educación matemática inspiraron el desarrollo de didácticas específicas en física, química y biología. En Chile, investigadores como Claudia Reyes continúan esta tradición, adaptando los marcos teóricos de Artigue a los desafíos locales de la educación científica.
La obra de Artigue demuestra que la educación científica de calidad requiere tanto dominio disciplinario como comprensión profunda de los procesos de enseñanza y aprendizaje. Su legado nos recuerda que la interdisciplinariedad efectiva no surge de diluir las disciplinas, sino de comprender y respetar sus especificidades epistemológicas mientras se construyen puentes entre ellas.
Referencias
- Artigue, M. (1991). “Épistémologie et didactique”. Recherches en Didactique des Mathématiques, 10(2-3), 241-286. Disponible en línea
- Artigue, M. (2002). “Learning mathematics in a CAS environment: the genesis of a reflection about instrumentation and the dialectics between technical and conceptual work”. International Journal of Computers for Mathematical Learning, 7(3), 245-274. DOI: 10.1023/A:1022103903080
- Artigue, M. (2020). “Didactic engineering in mathematics education”. En S. Lerman (Ed.), Encyclopedia of Mathematics Education. Springer. DOI: 10.1007/978-3-030-15789-0_44
- Brousseau, G. (1997). Theory of didactical situations in mathematics. Kluwer Academic Publishers
- Chevallard, Y. (1985). La transposition didactique. La Pensée Sauvage
- Karp, A. (Ed.) (2015). “Interview with Michèle Artigue”. En Leaders in Mathematics Education: Experience and Vision. Sense Publishers
- Menghini, M., Furinghetti, F., Giacardi, L., & Arzarello, F. (Eds.) (2009). The First Century of the International Commission on Mathematical Instruction (1908-2008). Roma: Istituto della enciclopedia Italiana. PDF disponible
- Artigue, M. (2009). “ICMI: A century at the interface between mathematics and mathematics education”. En el libro anterior, pp. 185-198
Este podcast fue apoyado en parte por la Agencia Nacional de Investigación y Desarrollo (ANID), Chile (ANILLO ATE220022; ALMA 31220004; FONDECYT 1211848) y Proyecto DGVM 3054 (PUCV).

